suivant: Mise en oeuvre du
monter: Présentation du problème
précédent: Outils utilisés
Table des matières
Note préliminaire :
Dans cette partie, on expose le modèle mathématique "idéal". Des limitations
techniques que nous expliquons plus bas, ne nous permettent pas d'implémenter la
résolution des équations régissant le système en temps réel. Ce modèle n'est
donc valable que si l'on dispose d'outils suffisamment puissants permettant
cette résolution.
Il s'agit en fait d'un problème de commande classique. Le processus consiste
en une tige articulée (pendule inversé) placée sur un chariot mobile, comme
l'illustre la figure (celle qu'il faut). La tige et le chariot ne peuvent se
mouvoir que dans un plan vertical, mais les deux mouvements sont sujets à
l'action du frottement.
L'objectif de commande est de maintenir le système à
l'intérieur d'une certaine zone 1.2 (appelée "zone de
viabilité") par un choix judicieux de forces horizontales 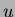 à appliquer au
chariot.
à appliquer au
chariot.
L'état du système est déterminé par 4 variables
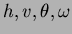 désignant respectivement la position horizontale du chariot (m), la vitesse du
chariot (m/s), la position angulaire de la tige (rad), la vitesse angulaire (rad/s).
En supposant une
distribution uniforme de poids dans la tige et l'absence d'effets élastiques,
les équations régissant le comportement du système peuvent s'écrire :
désignant respectivement la position horizontale du chariot (m), la vitesse du
chariot (m/s), la position angulaire de la tige (rad), la vitesse angulaire (rad/s).
En supposant une
distribution uniforme de poids dans la tige et l'absence d'effets élastiques,
les équations régissant le comportement du système peuvent s'écrire :
avec
où 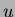 est la force (exprimée en N) appliquée au chariot,
est la force (exprimée en N) appliquée au chariot, 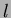 est la distance du
centre de masse de la tige au pivot (70 cm),
est la distance du
centre de masse de la tige au pivot (70 cm), 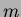 est la masse de la tige (120
g),
est la masse de la tige (120
g), 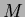 est la masse du chariot (600 g),
est la masse du chariot (600 g),
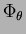 est le couple de
frottement du chariot sur le rail.
est le couple de
frottement du chariot sur le rail.
Si on disposait de capteurs fournissant les 4
variables d'état, des expériences en simulation pourraient être menées en
intégrant numériquement les équations ci-dessus (pas d'intégration 0.001s,
méthode de Runge-Kutta d'ordre 4).
Quand bien même on arriverait à faire des mesures de tous les paramètres du système,
la puissance brute de calcul du micro-contrôleur est tout de même limitée pour la résolution
numérique des équations et de la gestion effective du contrôle dynamique du pendule dans des tâches
parallèles. Par ailleurs, nous avons été confortés dans notre choix car des limitations intrinsèquement
techniques sont apparues lors de la construction de notre pendule qui nous obligent à exclure
l'implémentation du schéma de résolution numérique dans le RCX.




suivant: Mise en oeuvre du
monter: Présentation du problème
précédent: Outils utilisés
Table des matières
2001-01-11
![$\displaystyle \frac{1}{l . \left[ \frac{4}{3} -
\frac{m \, . \, cos^2 \theta}{m...
...^2 . sin \,\theta + \Phi_h}{m + M}
\right] - \frac{\Phi_\theta}{m . l } \right)$](img6.png)